二人若不同心,豈能同行呢?
獅子若非抓食,豈能在林中咆哮呢?
── 〈阿摩司書〉3章3節

「這很簡單啊,親愛的華生先生。」
福爾摩斯說完這句話之後,就以他著名的不簡單推理讓忠實助手聽得暈頭轉向。但福爾摩斯真正厲害的,不是由假設演繹出結論,而是歸納。歸納的運作方向和演繹相反,是從證據產生假設。

福爾摩斯另一段名言透露了他的歸納方式:「排除所有不可能之後,剩下的即使再不可能,也一定是真相。」福爾摩斯先歸納出幾種假設,再一一排除,(以排除法)演繹出正確的假設。歸納和演繹雖然是一體的兩面,但歸納一向比較神祕。由於這個緣故,福爾摩斯這些偵探才有工作可做。
然而近年來,在由證據產生假設、以及由結果得知原因的過程自動化領域,人工智慧專家已經有了大幅進展。很幸運地,我在這些進展的早期階段也盡了一份心力,開發出貝氏網路(Bayesian network)這種基本工具。本章將說明貝氏網路是什麼,介紹貝氏網路目前的幾種用途,同時討論貝氏網路引領我研究因果的曲折歷程。
電腦偵探波拿巴(Bonaparte)
2014年7月17日,馬航十七號班機由阿姆斯特丹史基普機場(Schiphol Airport)起飛前往吉隆坡,但這班飛機永遠到不了目的地。飛行三小時後,它和飛過烏克蘭上空的噴射機一樣,遭到俄製地對空飛彈擊落。機上共有兩百八十三名乘客和十五名組員,兩百九十八人全部罹難。
7月23日,首批遺體運抵荷蘭,荷蘭宣布當天是國殤日。但對於在荷蘭海牙法醫研究所(NFI)的調查人員而言,7月23日則是分秒必爭的起點。他們的工作是盡快辨識出遺體身分,以便交還親屬安葬。時間至關緊要,因為一天不確定遺體身分,親屬的悲痛就加深一層。
調查人員面臨許多困難。遺體燒傷嚴重,許多以福馬林保存,但福馬林會破壞DNA。此外,烏克蘭東部是戰區,法醫專家無法隨意到達墜機地點。新搜尋到的遺體陸續送達,時間長達十個月。最後,調查人員沒有罹難者的DNA紀錄,理由很簡單,因為罹難者不是罪犯。調查人員只能依靠部分相符來判定親屬關係。
幸運的是,NFI科學家擁有強大的工具奧援,這是一套最先進的罹難者辨識軟體,稱為波拿巴(Bonaparte)。這套軟體由位於奈梅亨(Nijmegen)的拉德伯德大學研究團隊於2000年代中期開發,運用貝氏網路綜合取自數名罹難者家屬的DNA資料。
在波拿巴這套軟體協助下,NFI於2014年12月前找到兩百九十八名罹難者中兩百九十四人的遺體。到2016年,這次空難中僅有兩名罹難者下落不明(而且都是荷蘭人)。
波拿巴軟體使用的機器推理工具是貝氏網路。貝氏網路在日常生活中影響我們的層面相當多,但大多數人沒有察覺。使用貝氏網路的地方包括語音辨識軟體、垃圾郵件過濾程式、氣象預報、探勘油井,以及美國食品藥物署批准醫療器材的過程等。在微軟Xbox上玩遊戲時,負責評定玩家分數的也是貝氏網路。如果你有手機,手機代碼必須以置信度傳播(belief propagation)解碼,以便從幾千個通話中分辨屬於這個門號的通話,而這種演算法則是為貝氏網路設計。另一家赫赫有名的公司谷歌,它的網路推廣長文特.瑟夫(Vint Cerf)曾經說:「我們是貝氏方法的超級使用者。」
在這一章中,我會細說貝氏網路的來龍去脈,從十八世紀的起源談到1980年代的發展,此外還會介紹目前貝氏網路的幾個應用範例。貝氏網路與因果圖間的關係很簡單:因果圖就是貝氏網路,圖中的箭頭代表直接或可能存在的因果關係,以箭頭方向為準。貝氏網路不一定有因果性,但這在許多用途中不重要。然而,如果打算提出關於貝氏網路的第二層或第三層查詢,就必須非常注意因果性並繪製因果圖。
貝斯牧師與逆機率問題
1985年我用湯瑪斯.貝斯(Thomas Bayes)為這種網路命名,貝斯牧師應該從來沒想過,他在1750年代提出的方程式,日後會被用來判別罹難者身分。當時他研究的是兩個事件的機率,其中一個事件(假設)發生在另一個事件(證據)之前。儘管如此,因果在他心裡仍然非常重要。事實上,讓他著手分析逆機率(inverse probability)的主要因素,就是因果。
貝斯是長老會牧師,生於1702年,卒於1761年,似乎是數學高手。他是英國人,但不信奉英國國教,所以無法進入牛津或劍橋等著名大學,而是在蘇格蘭大學接受教育,可能在那裡學了不少數學。後來他持續浸淫在數學中,返回英格蘭後還組成數學讀書會。
在一篇他去世後才發表的文章中,貝斯探討了最適合他來研究的問題 ── 比較數學和神學。先說明一下來龍去脈。1748年,蘇格蘭哲學家休謨撰寫論文《論奇蹟》(On Miracles),主張目擊者證詞無法證明奇蹟確實發生。儘管休謨聰明地沒有明講,但他說的奇蹟當然是指耶穌復活。(在此二十年前,神學家湯瑪斯.伍爾斯頓〔Thomas Woolston〕曾因為撰寫類似文章而遭控褻瀆入獄。)休謨的主要論點是:本質上不可靠的證據,無法否定「人死不能復生」這類擁有自然定律後盾的命題。

對貝斯而言,這個主張帶出一個既自然、又很福爾摩斯的問題:需要多少證據才能讓我們相信,某件我們認為不大可能的事真的發生過?一個假設何時會從不可能變成不大可能、甚至變成可能或幾乎一定會發生?這個問題雖然以機率語言表達,但刻意融入了神學意義。貝斯去世後,同教會牧師理查.普萊斯(Richard Price)在貝斯的遺物中發現這篇論文,將它連同他自己撰寫的導讀一起寄出發表,更清楚地說明了這一點:
我的目的是證明:我們有什麼理由相信萬物之中有固定法則,而萬事都是依這些法則發生?我們何以相信世界必然是某個智性之因的智慧與權能所導致的結果,從而肯定從最終因導出的推論足以證明上帝的存在?這篇論文解決的逆問題,能更直接適用於上述目的,這點很容易理解。因為它明確告訴我們,在任何具備特定順序或週期的事件中,我們用什麼理由認為這種週期或秩序,是源於自然界中穩定的原因或規則,而非源自機率的任何不規則性。
貝斯自己從來沒有在論文中探討過這點,普萊斯特別強調這些神學含意,或許是為了擴大貝斯這篇論文的影響力。但普萊斯特其實不需要這麼做。兩百五十年後,依然有人記得和討論貝斯的論文,原因不僅在於它的神學意義,還因為這篇論文證明我們可由結果演繹出某個原因的機率。如果知道原因,要估算出結果的機率相當容易,這是正向機率。但要反過來演繹(在貝斯的時代稱為「逆機率」問題),則困難得多。貝斯沒有解釋為什麼如此,而是把它視為不證自明,證明這是可行的,並且示範該怎麼做。
為了正確理解這個問題的本質,我們先來看看貝斯在1763年去世後出版的論文中舉的例子。假設我們在撞球桌上打出一顆球,讓它反彈多次,因此無法確定最後球會停在哪裡,則這顆球停在距離球桌左端小於x英尺處的機率是多少?如果知道球桌長度和球桌完全平坦光滑,這個問題相當容易解答(參見〈圖3.2〉上)。舉例來說,在12英尺長的斯諾克球桌上,這顆撞球停在距離球桌左端小於1英尺處的機率是1/12。而在8英尺長的花式撞球桌上,機率是1/8。
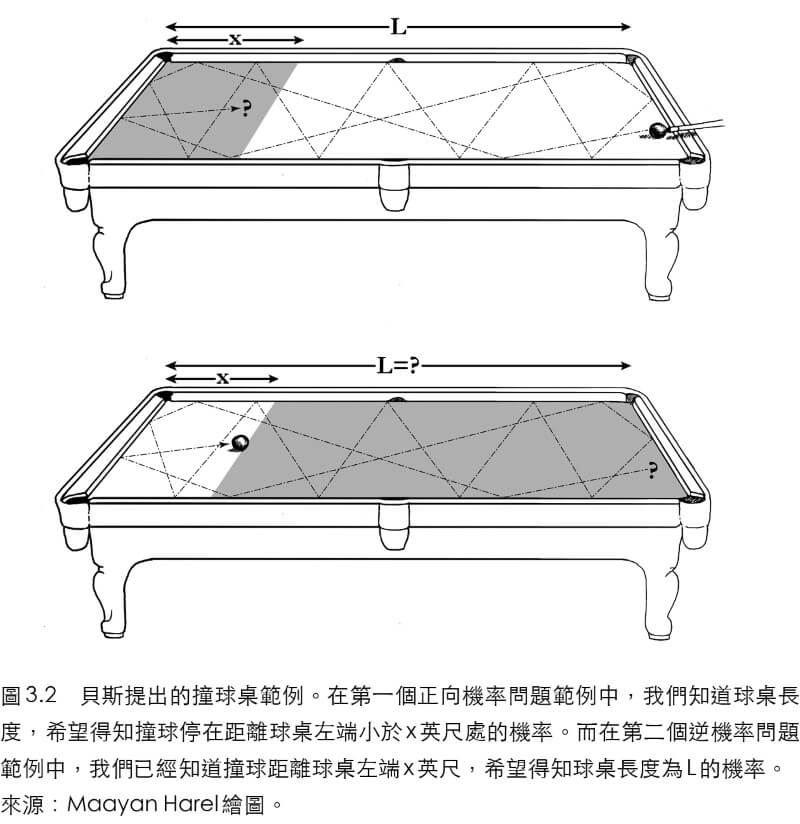
依據我們對物理學的理解,通常如果球桌長度是L英尺,則撞球停在距離左端小於x英尺處的機率為x/L。球桌長度(L)越長,撞球可能停留的範圍越大,所以機率越低。另一方面,如果x越大,符合的停留範圍也越大,所以機率越高。
現在來看看逆機率問題。我們已知撞球停留位置為距離左端x=1英尺,但不知道球桌長度L(參見〈圖3.2〉下)。貝斯牧師問,球桌長度為100英尺(假設)的機率為何?依據常識,L為50英尺的機率比100英尺高,原因是球桌長度越長,撞球越不容易距離左端那麼近,但機率究竟高出多少?「直覺」或「常識」都無法提供明確的指引。
正向機率(已知L時計算x的機率)為何在心理上,遠比已知x時計算L的機率容易得多?在這個範例中,差別來自L是原因,x是結果。如果已經知道原因(例如巴比把球丟向窗戶),大多數人都預料得到結果(窗戶應該會被球打破)。人類的認知是朝這個方向推演。但如果已經知道結果(窗戶被打破),則我們會需要更多資訊才能演繹出原因(是哪個小孩丟球打破窗戶,或窗戶是被球打破等)。我們必須擁有福爾摩斯的頭腦,才能推斷出所有可能原因。貝斯著手破除這個認知差異,解說一般人應該如何估算逆機率。








